-
 Naturopathy
Naturopathy
-
 Trojan horse
Trojan horse
-
 Condyloid
Condyloid
-
 Australopithecus
Australopithecus
-
 Crystalline state
Crystalline state
-
 Clinopyroxene
Clinopyroxene
-
 DMB
DMB
-
 Backdoor
Backdoor
-
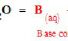 Acid
Acid
-
 Isomerism
Isomerism
-
 MIME
MIME
-
 Zodiacal light
Zodiacal light
-
 Auscultation
Auscultation
-
 Petiole
Petiole
-
 LCoS
LCoS
-
 Semaphore
Semaphore
-
 Otherness
Otherness
-
 Quinolone
Quinolone
-
 Android
Android
-
 DSS
DSS
-
 Bioluminescence
Bioluminescence
-
 Climax community
Climax community
-
 Julian calendar
Julian calendar
-
 Secondary energy
Secondary energy
-
 Tectite
Tectite
-
 Resilient
Resilient
-
 Lagrangian
Lagrangian
-
 Holohedry
Holohedry
-
 Phytohormone
Phytohormone
-
 Starch
Starch
String theory
String theory was initially conceived as an alternative to describe strong interaction: for example, the process of a collision between two hadrons would be described as a collision between two strings which, breaking, would form other hadrons. In 1968, Gabriele Veneziano found a mathematical formula to describe such a process; these theories, called dual models, gave rise to great hopes.
A few years later a competing theory appeared: quantum chromodynamics. Then in 1969, the success of the SLAC accelerator experiments (Stanford) and the demonstration of asymptotic freedom in 1973 imposed the choice of quantum chromodynamics and, apart from a few exceptions, most physicists abandoned dual models.
Thus in 1975, Joël Scherk and John Schwarz showed that string theory required a particle of spin 2 and zero mass that could be identified as the graviton, i.e. a quantum of gravitation. Strings could therefore be more suitable to describe gravitational interaction than strong interaction.
In 1984, John Schwarz and Michel Green built a coherent string theory model which incorporated parity violation and which showed no anomalies in 10-dimensional space-time. String theory gained the renewed interest of physicists in 1985 when Edward Witten showed that the number of dimensions could be reduced from 10 to 4 while preserving supersymmetry, on condition that the 6 extra dimensions were compacted into a special space called a Calabi-Yau manifold. In the same year, David Gross and his team managed to build models, called heterotic strings, that contained gauge theories. The dream of a theory of everything was at last taking shape!
Since then, interest in string theory has grown ceaselessly and has also won over the community of mathematicians. The mathematical formalism of string theory is indeed very complex and heterogeneous and has points of convergence with various branches of mathematics: theorems from one branch have for example been demonstrated using tools from another branch.
Unlike quantum field theory where the particles are described by points, in string theory a particle is made up of a string of extremely small size (10-33 cm), a sort of closed or open lace that moves and vibrates. If the string vibrates in a certain mode it describes an electron; and if it vibrates in another mode it describes a quark, and so on.
What is string theory?
In field theory a moving particle traces a line but in string theory it traces a two-dimensional surface, a tube. In the latter case the concepts are more abstract: for on this two-dimensional surface called the surface of the Universe are defined abstract mathematical entities: fields that form the coordinates of space-time. The number of fields defined on the surface of the Universe then gives the dimensions of space-time. Supersymmetry occupies a major place in string theory: it facilitates the stability of the theory and the description of fermions, particles with half-integer spin.
In the latter case the Feynman diagrams, which describe interactions between the particles, become a network of intersecting tubes. Now in quantum field theory the infinite results that appear during loop calculations are due to points of interaction between three lines (a vertex). In string theory, the intersection is no longer a point but a two-dimensional surface and the infinite quantities no longer appear: although there is no mathematical proof yet, there are strong reasons to believe that string theory is finite.
Why string theory?
String theory is currently the only theory to treat gravity in quantum fashion. In principle it unifies all the fundamental interactions. It is only valid if space-time has 10 dimensions, because of what are called anomalies: a classical theory may have a certain symmetry; but when the laws of quantum mechanics are introduced this symmetry is not kept without introducing certain constraints. An anomaly is a classical symmetry that is no longer respected at a quantum level. For example, in the Standard Model, the weak interaction, violating parity, could lead to a right-left anomaly (a chiral gauge anomaly) and threaten the renormalisation of the theory if the sum of the electric charges of a family of leptons and quarks were not nil. Fortunately, this does not happen: if we add the electrical charges of the up and down quarks (each with three colours) to the electrical charges of the electron and neutrino leptons, we obtain: 3 x (2/3-1/3) + (-1) + 0 = 0.
What is an anomaly?
Analogously to this there are symmetries in string theory: the physics described by the theory must not depend on the way we choose the coordinates on the surface of the Universe. The theory is said to be invariant to the choice of coordinates. The theory of invariance has cropped up several times: Einstein's theory of gravitation is invariant to a change in space-time coordinates, gauge theories are invariant to a change in gauge. If quantum laws are introduced into string theory, the invariance of the theory to changes in the coordinates of the surface of the Universe is threatened (it presents an anomaly), unless the dimension of space-time is equal to 10.
Five different string theories can thus be built in 10-dimensional space-time. In physicists' jargon these are called: type I, type IIA, type IIB, heterotic E8xE8 and heterotic SO(32). In type I theory strings are open or closed and in the other cases only closed. As their names indicate, the heterotic SO(32) theory contains the rotational gauge group SO(32) (acting in a space of internal symmetry described by the matrices of rotation of a 32-dimensional internal space) and the heterotic E8xE8 theory contains the special gauge group E8xE8 . The latter could contain the gauge groups of the Grand Unification Theory and is therefore a potential candidate for the unification of the fundamental interactions.
Credits: www.diffusion.ens.fr/vip
Sites on string theory:
Latest
Fill out my online form.



