-
 Meteosat
Meteosat
-
 Gymnosperm
Gymnosperm
-
 IMAP
IMAP
-
 Phases of a planet
Phases of a planet
-
 Galactocentric coordinate
Galactocentric coordinate
-
 Glucose-6-phosphate isomerase
Glucose-6-phosphate isomerase
-
 Sex glands
Sex glands
-
 Catadioptric
Catadioptric
-
 Cloning
Cloning
-
 Data switch
Data switch
-
 Einstein's box
Einstein's box
-
 Booster
Booster
-
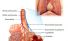 Respiration
Respiration
-
 Invasive
Invasive
-
 Osteosarcoma
Osteosarcoma
-
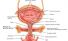 Bladder
Bladder
-
 Hox gene
Hox gene
-
 Hot spring
Hot spring
-
 Water-borne diseases
Water-borne diseases
-
 Tail assembly
Tail assembly
-
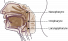 Pharynx
Pharynx
-
 Keesom force
Keesom force
-
 Maritime swamp
Maritime swamp
-
 Anaerobic
Anaerobic
-
 Legume
Legume
-
 Anti-aliasing
Anti-aliasing
-
 Open source software
Open source software
-
 Granulite
Granulite
-
 Cluster
Cluster
-
 Aarhus Protocol
Aarhus Protocol
Maxwell's demon
Maxwell's demon is a thought experiment proposed by James Maxwell in 1867 to violate the second law of thermodynamics.
Maxwell was interested in the kinetic theory of gases in which the thermodynamic properties of gases were reduced to those of the mechanics of a very large number of molecules. Heat was then treated as a particular form of energy in the form of the disordered agitation of the molecules. The greater the agitation, the higher the temperature of the gas.
The trouble is, thermodynamics - the science of energy transformation, and especially the rules for the transformation of heat into useful work - implies a direction for the flow of time and limits the possible transformations of energy and matter. Heat does not flow spontaneously from a cold body to a hot body, it cannot be completely transformed into work if the temperature is the same everywhere in the system, a broken vase does not stick itself together again spontaneously, a drop of ink in a glass of water does not re-form itself after diffusing.
Now, if the reduction to thermodynamics is to be taken seriously, this is highly paradoxical. The equations of motion of particles in a gas, or of the particles making up any other material body, do not reflect the difference between motion in a given direction of time and motion in the opposite direction. This means that it is just as likely that a vase will break as it will stick itself together spontaneously, or that a drop of ink diffusing in a glass of water will return to its initial concentration state. The second law would therefore be true only approximately, on average and should be violable even if very difficultly in practice. Except of course for an analogue of Laplaces's demon, that is, the famous Maxwell's demon!
Imagine a box initially with molecules of a real gas gathered together in one corner; thermal agitation, hence the second law of thermodynamics, will ensure that the gas diffuses until it occupies the entire box volume uniformly. This is a so-called thermodynamic equilibrium situation in which the gas shows no tendency to return to a single corner of the box. This allows to define a direction for the flow of time.
Now imagine a wall dividing the box into two parts, one of which, B, is larger than the other, A. Part A is the initial zone where the gas was before diffusing. A small hole is made in this wall with a door that a little demon can close or open at will.
The gas is initially distributed uniformly in each part of the box, but as soon as a molecule moves towards the hole, from B to A, the demon leaves the door open. Conversely, if the molecule is moving from A towards B, the demon closes the door.
It is easy to see that after a certain time the gas will once again be in the corner of the box and will have returned to a situation of non-equilibrium. The second law of thermodynamics has therefore been violated!
 In aMaxwell's demon separates two types of initially mixed molecule, in b it puts all the molecules in one part of the box />
In aMaxwell's demon separates two types of initially mixed molecule, in b it puts all the molecules in one part of the box />
In aMaxwell's demon separates two types of initially mixed molecule, in b it puts all the molecules in one part of the box />
Actually, no! A few years later, Léon Brillouin and Léo Szilard settled the matter. To observe the molecules the demon would need to expend energy to illuminate them. A close analysis then shows that the second law, having been chased out of the door, returns through the window!

James Clerk Maxwell
Latest
Fill out my online form.



